
El ruido II. Transmisión I
Hojas Técnicas
En la Hoja Técnica "El ruido I. Los Decibelios" se definía el sonido, se describía el decibelio y se indicaba la medida objetiva del ruido. Aquí seguiremos con el tema, empezando con la medición subjetiva del sonido.
Lo que interesa conocer es cómo responde el oído humano ante un sonido y saber cuán molesto resulta. Existe una evidente correlación entre la intensidad mecánica y la intensidad subjetiva pero no es fácil obtener una curva que ligue ambas magnitudes, sobre todo por la gran variedad de individuos que existen y la gran diferencia de percepción de unos a otros.
El primer experimento que se hizo fue comparar un sonido puro de 1.000 Hz y de una determinada presión sonora con otro de otra frecuencia y variar su intensidad hasta que el observador medio considerara que eran iguales. Así, por ejemplo, experimentaron con un sonido puro a 1.000 Hz y una presión de 30 dB comparándolo con otro de 100 Hz; el observador medio consideró que eran iguales cuando éste segundo tenía 60 dB. De este sonido dijeron que tenía 30 FONOS. Se dice, pues, que un sonido tiene x FONOS cuando parece de igual intensidad que otro de 1.000 Hz con una presión sonora de x dB.
Del modo descrito, se experimentaron diferentes presiones a 1.000 Hz y diferentes frecuencias determinándose las curvas isofónicas de la Fig. 1 llamadas de Fletcher y Munson.
FONOS
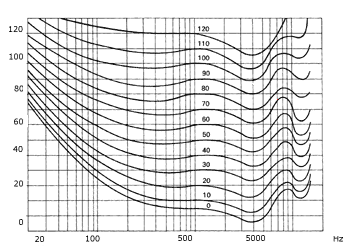
Fig. 1. Curvas de Fletcher y Munson
Del examen de estas curvas se deduce que la sensibilidad del oído humano disminuye para frecuencias muy bajas y muy altas, teniendo la máxima para unos 4.000 Hz. Además, para complicar las cosas, este fenómeno es más acusado a niveles de presión sonora bajos que a los altos.
Se ha construído aparatos para medir el sonido (sonómetros) que atenúan la señal captada, de acuerdo con la frecuencia, para simular así las curvas anteriores. Las atenuaciones normalizadas son las representadas en la Fig. 2 llamadas A, B, C y D.
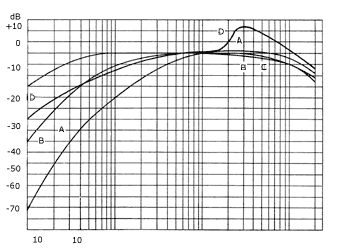
Fig. 2. Curvas de ponderación llamadas A-B-C y D
La A se utilizaría en el caso de sonidos de poca intensidad, la B para medios y la C para altos. En la práctica, no obstante, sólo se utiliza la A para todos los niveles, ya que la B y la C no han proporcionado resultados satisfactorios debido, principalmente, a que los sonidos con que se obtuvieron las curvas de Fletcher y Munson eran puros y los sonidos en la práctica son mucho más complejos. La curva D sirve sólo para medir el ruido de los aviones a reacción.
Si se desean más detalles de una señal compleja, la gama de frecuencias de 20 Hz a 20 K Hz se divide en octavas o tercios de octava. Este proceso se conoce por "Análisis de Frecuencia" y los resultados se presentan en unos gráficos como el de la Fig. 3, denominados espectrogramas.
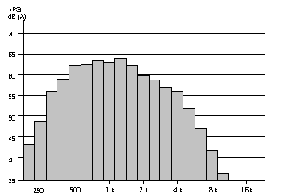
Fig. 3. Espectrograma
Conocida ya la diferencia entre presión sonora y potencia sonora, así como las fórmulas de relación que liga a ambas en "Campo libre" sin reflexiones por la proximidad de las paredes, y por otra parte el que un ventilador produce ruido en su funcionamiento, veamos aproximadamente qué potencia sonora emite el aparato mediante el uso del nomograma de la Fig. 4.
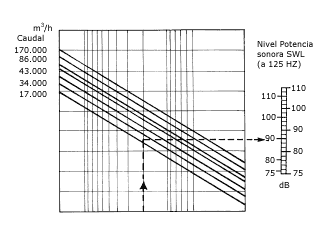
Fig. 4. Potencia sonora de un ventilador
Supongamos un ventilador axial que da 4000 m³/h a una presión de 500 Pa (50 mm c.d.a.). Según el nomograma, a 125 Hz le corresponde un SWL de 90 dB. Su espectro será el que figura al pie, que se ha obtenido sumando los 90 dB a las correcciones indicadas en la tabla correspondiente.
Tabla de correcciones a sumar
1. Influencia de las paredes
Si la fuente sonora está situada cerca del suelo, Fig. 5, el nivel de presión sonora en un punto A es suma del sonido directo y del reflejado por el suelo. En este caso, en que la propagación es semiesférica, la relación entre Lp y Lw es:
Así, si Lw = 80 dB y r = 10 m, el nivel de presión sonora en A valdrá:
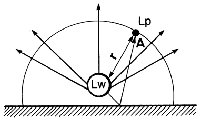
Fig. 5. Nivel de presión sonora
En el caso en que la fuente esté encerrada en una habitación, Fig. 6, el problema no es tan sencillo. En efecto, el nivel de presión sonora en un punto será la composición del directo y del de las sucesivas reflexiones que tienen lugar en las paredes, suelo y techo.
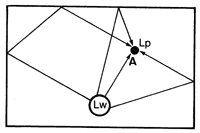
Fig. 6. Nivel de presión sonora
Es evidente que el valor del sonido reflejado, depende del grado de absorción de las paredes, suelo y techo, por lo que será necesario introducir un factor que recoja este extremo. Este factor, representado por R, se llama "constante de la sala" y su valor en m² es el siguiente:
S = Superficie total de las paredes + techo + suelo (m²).
a1, a2, a3 = Coeficientes de absorción de las superfícies reflectantes (paredes, suelo, ...).
S1, S2, S3 = Superficie en m² correspondiente a cada grado de absorción.
Una vez calculado el valor de R y conocido el factor de directividad Q, que nos da la Tabla 1, estaremos en condiciones de utilizar el gráfico de la Fig. 7, el cual para cada distancia r, del punto considerado A a la fuente, obtenemos un valor en dB que debemos sumar al nivel de potencia sonora Lw, para conocer el nivel de presión sonora Lp en el punto A.
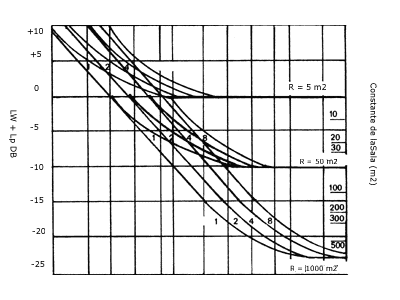
Fig. 7. Gráfica para conocer el nivel de presión sonora Lp en el punto A
Supongamos, por ejemplo, una habitación paralepipédica, Fig. 8, de 5 m de ancho por 7 m de largo y por 3 m de alto, y que el coeficiente de absorción es 0,8 para las paredes, 0,6 para el techo y 0,2 para el suelo.
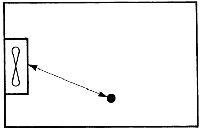
Fig. 8. Habitación paralepipédica
Si en el centro de una pared está instalado un ventilador de 60 dB de potencia sonora, el nivel de presión a 2 m del ventilador valdrá:
El coeficiente medio de absorción será:
La constante de la sala valdrá
Según la Tabla 1, Q = 2. Con estos datos, en la Fig. 7 encontramos
para una distancia a la fuente de 2 m. Por tanto :
2. Ruido a través de canalizaciones
Antes se ha señalado un procedimiento para calcular la presión que existe en un punto de un local, conociendo la situación y potencia de la fuente de ruido que existe en el mismo. Debe ahora resolverse el mismo problema, pero considerando que el ruido se transmite al local en cuestión a través de una canalización, tal como ocurre en las instalaciones de aire acondicionado.
Debe considerarse el orificio de descarga como fuente de ruido que emite una potencia sonora igual a la del elemento emisor, disminuída por las atenuaciones del conducto.
Para expresar con más claridad el proceso a seguir para calcular las atenuaciones que se producen, lo explicaremos conjuntamente con la resolución de un ejemplo.
Supongamos que un ventilador, Fig. 9 suministra una cantidad de aire que se distribuye en varios canales. La potencia sonora total emitida tiene un espectro reflejado en la Tabla 2.
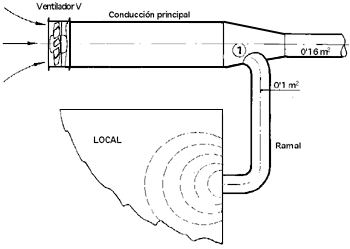
Fig. 9. Esquema ventilador
Si al local considerado va a parar sólo el caudal del ramal 1, es evidente que no todo el ruido del ventilador le alcanzará. Se puede calcular el espectro de la potencia de la onda propagada por el conducto que interesa, restando del ventilador el valor determinado por el uso de la gráfica de la Fig. 10.

Fig. 10. Cálculo del espectro de la onda propagada por el conducto
En el ejemplo, una vez calculado, resulta para ß un valor de 0,385 y la atenuación correspondiente de 4 a ß. Este valor debe sustraerse de cada uno de los del espectro del ventilador para cada frecuencia, resultando, para el local, el espectro reflejado en la Tabla 3.

Lo que interesa conocer es cómo responde el oído humano ante un sonido y saber cuán molesto resulta. Existe una evidente correlación entre la intensidad mecánica y la intensidad subjetiva pero no es fácil obtener una curva que ligue ambas magnitudes, sobre todo por la gran variedad de individuos que existen y la gran diferencia de percepción de unos a otros.
El primer experimento que se hizo fue comparar un sonido puro de 1.000 Hz y de una determinada presión sonora con otro de otra frecuencia y variar su intensidad hasta que el observador medio considerara que eran iguales. Así, por ejemplo, experimentaron con un sonido puro a 1.000 Hz y una presión de 30 dB comparándolo con otro de 100 Hz; el observador medio consideró que eran iguales cuando éste segundo tenía 60 dB. De este sonido dijeron que tenía 30 FONOS. Se dice, pues, que un sonido tiene x FONOS cuando parece de igual intensidad que otro de 1.000 Hz con una presión sonora de x dB.
Del modo descrito, se experimentaron diferentes presiones a 1.000 Hz y diferentes frecuencias determinándose las curvas isofónicas de la Fig. 1 llamadas de Fletcher y Munson.
FONOS

Fig. 1. Curvas de Fletcher y Munson
Del examen de estas curvas se deduce que la sensibilidad del oído humano disminuye para frecuencias muy bajas y muy altas, teniendo la máxima para unos 4.000 Hz. Además, para complicar las cosas, este fenómeno es más acusado a niveles de presión sonora bajos que a los altos.
Se ha construído aparatos para medir el sonido (sonómetros) que atenúan la señal captada, de acuerdo con la frecuencia, para simular así las curvas anteriores. Las atenuaciones normalizadas son las representadas en la Fig. 2 llamadas A, B, C y D.

Fig. 2. Curvas de ponderación llamadas A-B-C y D
La A se utilizaría en el caso de sonidos de poca intensidad, la B para medios y la C para altos. En la práctica, no obstante, sólo se utiliza la A para todos los niveles, ya que la B y la C no han proporcionado resultados satisfactorios debido, principalmente, a que los sonidos con que se obtuvieron las curvas de Fletcher y Munson eran puros y los sonidos en la práctica son mucho más complejos. La curva D sirve sólo para medir el ruido de los aviones a reacción.
Si se desean más detalles de una señal compleja, la gama de frecuencias de 20 Hz a 20 K Hz se divide en octavas o tercios de octava. Este proceso se conoce por "Análisis de Frecuencia" y los resultados se presentan en unos gráficos como el de la Fig. 3, denominados espectrogramas.

Fig. 3. Espectrograma
Conocida ya la diferencia entre presión sonora y potencia sonora, así como las fórmulas de relación que liga a ambas en "Campo libre" sin reflexiones por la proximidad de las paredes, y por otra parte el que un ventilador produce ruido en su funcionamiento, veamos aproximadamente qué potencia sonora emite el aparato mediante el uso del nomograma de la Fig. 4.

Fig. 4. Potencia sonora de un ventilador
Supongamos un ventilador axial que da 4000 m³/h a una presión de 500 Pa (50 mm c.d.a.). Según el nomograma, a 125 Hz le corresponde un SWL de 90 dB. Su espectro será el que figura al pie, que se ha obtenido sumando los 90 dB a las correcciones indicadas en la tabla correspondiente.
Tabla de correcciones a sumar
| Banda de Octavas | Hz | 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 |
| Axial | dB | +1 | 0 | +1 | 0 | -1 | -4 | -9 | -15 |
| Centrífugo | dB | +2 | 0 | -3 | -4 | -11 | -16 | -21 | -26 |
1. Influencia de las paredes
Si la fuente sonora está situada cerca del suelo, Fig. 5, el nivel de presión sonora en un punto A es suma del sonido directo y del reflejado por el suelo. En este caso, en que la propagación es semiesférica, la relación entre Lp y Lw es:
Lp = Lw - 20 log r - 8 dB
Así, si Lw = 80 dB y r = 10 m, el nivel de presión sonora en A valdrá:
Lp = 80 - 20 log 10 - 8 = 52 dB

Fig. 5. Nivel de presión sonora
En el caso en que la fuente esté encerrada en una habitación, Fig. 6, el problema no es tan sencillo. En efecto, el nivel de presión sonora en un punto será la composición del directo y del de las sucesivas reflexiones que tienen lugar en las paredes, suelo y techo.

Fig. 6. Nivel de presión sonora
Es evidente que el valor del sonido reflejado, depende del grado de absorción de las paredes, suelo y techo, por lo que será necesario introducir un factor que recoja este extremo. Este factor, representado por R, se llama "constante de la sala" y su valor en m² es el siguiente:
R = S × a / 1 - a
S = Superficie total de las paredes + techo + suelo (m²).
a = (S1 a1 + S2 a2 + S3 a3 + ...) / S
a1, a2, a3 = Coeficientes de absorción de las superfícies reflectantes (paredes, suelo, ...).
S1, S2, S3 = Superficie en m² correspondiente a cada grado de absorción.
Una vez calculado el valor de R y conocido el factor de directividad Q, que nos da la Tabla 1, estaremos en condiciones de utilizar el gráfico de la Fig. 7, el cual para cada distancia r, del punto considerado A a la fuente, obtenemos un valor en dB que debemos sumar al nivel de potencia sonora Lw, para conocer el nivel de presión sonora Lp en el punto A.
|
||||||||||
| Tabla 1. Posición de Factor "Q" de la fuente Directividad |

Fig. 7. Gráfica para conocer el nivel de presión sonora Lp en el punto A
Supongamos, por ejemplo, una habitación paralepipédica, Fig. 8, de 5 m de ancho por 7 m de largo y por 3 m de alto, y que el coeficiente de absorción es 0,8 para las paredes, 0,6 para el techo y 0,2 para el suelo.

Fig. 8. Habitación paralepipédica
Si en el centro de una pared está instalado un ventilador de 60 dB de potencia sonora, el nivel de presión a 2 m del ventilador valdrá:
El coeficiente medio de absorción será:
a = (72 x 0,8 + 35 x 0,6 + 35 x 0,2) / (72 + 35 + 35) = 0,602
La constante de la sala valdrá
R = (142 x 0,602) / (1 - 0,602) = 214,7
Según la Tabla 1, Q = 2. Con estos datos, en la Fig. 7 encontramos
Lw + Lp = -12 dB
para una distancia a la fuente de 2 m. Por tanto :
Lp = 60 - 12 = 48 dB
2. Ruido a través de canalizaciones
Antes se ha señalado un procedimiento para calcular la presión que existe en un punto de un local, conociendo la situación y potencia de la fuente de ruido que existe en el mismo. Debe ahora resolverse el mismo problema, pero considerando que el ruido se transmite al local en cuestión a través de una canalización, tal como ocurre en las instalaciones de aire acondicionado.
Debe considerarse el orificio de descarga como fuente de ruido que emite una potencia sonora igual a la del elemento emisor, disminuída por las atenuaciones del conducto.
Para expresar con más claridad el proceso a seguir para calcular las atenuaciones que se producen, lo explicaremos conjuntamente con la resolución de un ejemplo.
Supongamos que un ventilador, Fig. 9 suministra una cantidad de aire que se distribuye en varios canales. La potencia sonora total emitida tiene un espectro reflejado en la Tabla 2.

Fig. 9. Esquema ventilador
|
||||||||||||||||||
| Tabla 2. Espectro del ventilador V |
Si al local considerado va a parar sólo el caudal del ramal 1, es evidente que no todo el ruido del ventilador le alcanzará. Se puede calcular el espectro de la potencia de la onda propagada por el conducto que interesa, restando del ventilador el valor determinado por el uso de la gráfica de la Fig. 10.

Fig. 10. Cálculo del espectro de la onda propagada por el conducto
En el ejemplo, una vez calculado, resulta para ß un valor de 0,385 y la atenuación correspondiente de 4 a ß. Este valor debe sustraerse de cada uno de los del espectro del ventilador para cada frecuencia, resultando, para el local, el espectro reflejado en la Tabla 3.
|
||||||||||||||||||
| Tabla 3. Espectro del ruido en el local |

 Extractores de baño
Extractores de baño Ventiladores en línea
Ventiladores en línea Extractores para Cristal o Pared
Extractores para Cristal o Pared VMC
VMC Cajas de Ventilación
Cajas de Ventilación Ventiladores de tejado
Ventiladores de tejado Recuperadores de Calor
Recuperadores de Calor Extractores de cocina
Extractores de cocina Campanas y grupos para cocinas
Campanas y grupos para cocinas Ventiladores de confort
Ventiladores de confort Tratamiento de aire
Tratamiento de aire Calefacción de instalación
Calefacción de instalación Calefacción doméstica portatil
Calefacción doméstica portatil Unidades de tratamiento de aire
Unidades de tratamiento de aire Ventiladores helicoidales tubulares
Ventiladores helicoidales tubulares Recuperadores de Calor
Recuperadores de Calor Ventiladores de confort
Ventiladores de confort Secamanos y Secadores de cabello
Secamanos y Secadores de cabello Ventiladores helicoidales murales
Ventiladores helicoidales murales Ventiladores Centrífugos
Ventiladores Centrífugos Extractores desenfumage
Extractores desenfumage Ventilación de parkings
Ventilación de parkings Extractores para atmósferas explosivas ATEX
Extractores para atmósferas explosivas ATEX Cortinas de aire
Cortinas de aire Calefacción industrial
Calefacción industrial Rodete álabes curvados hacia atrás
Rodete álabes curvados hacia atrás Rodete de álabes curvados hacia atrás de alta presión
Rodete de álabes curvados hacia atrás de alta presión Rodete de álabes curvados hacia adelante
Rodete de álabes curvados hacia adelante Rodete de álabes curvados hacia adelante (multipala)
Rodete de álabes curvados hacia adelante (multipala) Rodete de álabes curvados hacia atrás de doble aspiración
Rodete de álabes curvados hacia atrás de doble aspiración Rodete álabes radiales para transporte de materia
Rodete álabes radiales para transporte de materia Ventiladores centrífugos para hornos
Ventiladores centrífugos para hornos Ventiladores helicoidales
Ventiladores helicoidales Accesorios de montaje
Accesorios de montaje Accesorios eléctricos
Accesorios eléctricos

